Ultimate Desmos guide for Digital SAT along with 20 Practice Questions

Nail the Digital SAT Using Desmos

The Digital SAT brings a new set of opportunities for test-takers, especially with the integration of tools like Desmos, the graphing calculator. Leveraging Desmos effectively can significantly enhance your problem-solving speed and accuracy.

Below, you'll find 20 expertly curated questions, designed to cover a wide variety of problem types you might encounter on the SAT. These questions not only highlight the breadth of Desmos’ capabilities but also ensure you're prepared to solve them confidently, Stay tuned for these must-solve Desmos practice questions for SAT, where you'll use an integrated Desmos calculator to master the essential skills. With this practice, you'll be equipped to tackle any math challenge the SAT throws your way!

But first, here’s a quick guide to the 10 essential Desmos skills, along with practice examples to help you master them:

1. Solving Equations and Systems of Equations

• Use Desmos to quickly graph linear or quadratic equations and find their intersections, which represent the solutions.
• Solve systems of equations by plotting both equations and identifying their intersection points.
  
  

2. Finding Intercepts

• Graph equations to identify the x-intercept (where the graph crosses the x-axis) and the y-intercept (where it crosses the y-axis).
• This is especially useful for linear and quadratic functions.
• For word problems, Desmos can help you interpret intercepts. For instance, the x-intercept might represent when a quantity reaches zero, and the y-intercept could represent the initial value of a function.
  

3. Evaluating Functions

• Input a function into Desmos and evaluate specific values by tracing the graph or typing the value directly.
  

4. Inequalities

• Shade solution regions for inequalities to visually verify answers for SAT problems involving ranges or constraints.
• To find the common solution region for two or more inequalities, input them together into Desmos. For example, plotting 𝑦 > 2 𝑥 + 1 and 𝑦 < − 𝑥 + 4 will display overlapping shaded regions.
  

5. Mean, Median, and Regression Analysis

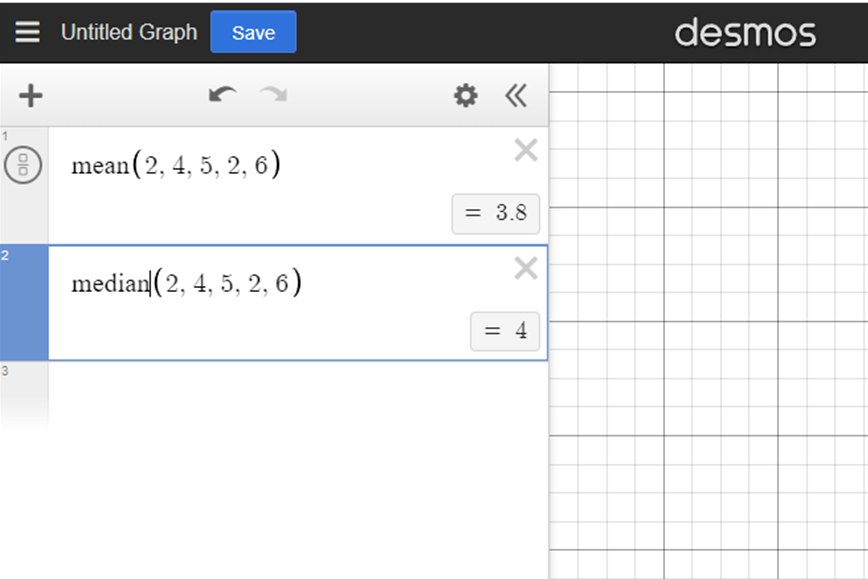
• Use Desmos to input data points and calculate regression lines or analyze scatterplots for mean and median.
• Plot scatterplots to identify trends and interpret statistical data visually.
  

6. Equations of Circles

• Input circle equations in standard form to verify their center and radius quickly. This is useful for geometry-related SAT questions.
  

7. Domains and Ranges

• Visualize domains and ranges of functions by observing the limits of the graph along the x-axis and y-axis.
  

8. Maximum and Minimum Values

• Identify the highest or lowest point of a graph, particularly for quadratic functions.
  

9. Percents and Quick Arithmetic

• Use Desmos' calculator feature for quick percent calculations or to perform operations like addition, subtraction, and multiplication.
• For routine calculations, Desmos can often be faster than a handheld calculator since it eliminates the need to switch devices or navigate physical buttons. You can simply type directly into Desmos.
  

10. Sliders

• Use sliders to dynamically change variables in equations and observe how graphs transform. This can help in understanding problem scenarios where variables change.
  

Let's Practice with Desmos for SAT!

To fully unlock Desmos' potential, it’s crucial to practice a curated range of problems that reflect the diverse ways it can be utilized on test day. Below, you'll find 20 expertly curated questions, designed to cover a wide variety of problem types you might encounter on the SAT. These questions not only highlight the breadth of Desmos’ capabilities but also ensure you're prepared to solve them confidently.

Ready to take on the challenge? Dive into this carefully curated 20-question challenge and put your Desmos skills to the test. Each problem comes with an integrated Desmos calculator to help you explore, solve, and analyze as you go. While there’s no strict time limit, pushing yourself to complete it within 45 minutes can make the practice more realistic and test-like. So, how many can you get right? Use the score calculator at the end to predict your SAT score and track your progress. Let’s get started—your SAT success begins now!

Question 1.

Solution 1.

• Open Desmos and type the equation directly: x = 70 / (x + 3).
• Observe where the graph intersects the x-axis.
• Identify the negative x-intercept, which is −10.

Question 2.

Solution 2.

• Input the function: f(x) = 27 * (2/3)^x.
• Look where the graph intersects the y-axis (x=0).
• The y-intercept is (0,27).

Question 3.

Solution 3.

• Input the formula: 104 = 1/2 (x - 3) x.
• Observe the two solutions where the graph intersects the x-axis.
• Select the positive solution since x represents a length B. 16.

Question 4.

Solution 4.

• Enter the points into a table in Desmos.
• Use the regression feature: y1 ~ a * b^x1.
• Desmos calculates the equation C. y = 740⋅ (1+ 0.005) ^x

Question 5.

Solution 5.

• Enter both equations: y = 7x and y = x + 18.
• Identify the intersection point visually.
• The lines intersect at one point.B. 1

Question 6.

Solution 6.

• Enter both equations into Desmos.
• Observe the intersection point.
• The x-coordinate of the intersection is the solution. A. -6

Question 7.

Solution 7.

• Enter the function: f(x) = 12x^2 - 30x - 162.
• Click on the vertex (minimum point).
• The x-coordinate of the vertex is the answer.1.25

Question 8.

Solution 8.

• Enter y=7x+5y and the point (0,0) in Desmos.
• Add (4,n) with a slider for n.
• Adjust n until the slope of the line through the two points matches 7. 28
  

Question 9.

Solution 9.

• Enter the parabola and the line 𝑦 = 𝑃 with a slider for 𝑃
• Adjust 𝑃 until the line intersects the parabola at exactly one point.-9.8

Question 10.

Solution 10.

• Use median (21, 23, 24, 25, 26, 28, 32, 34, 37) in Desmos.
• The output gives the median 26

Question 11.

Solution 11.

• Enter both expressions as functions in Desmos.
• Adjust 𝑟 until the graphs overlap completely.
• The value of 𝑟 is A. 8

Question 12.

Solution 12.

• Enter g(x)=6+x^3.
• Evaluate g(3) directly in Desmos.
• The result is 33.

Question 13.

Solution 13.

• Enter h(t)=−16t^2+96t+100.
• Restrict t≥0 to focus on relevant values.
• Observe the y-intercept (t=0), which is D. 100.

Question 14.

Solution 14.

• Enter g(x)=x^2−4
• Create a table and input the x-values.
• Observe corresponding g(x) values.
• B. x | 0 | 2 | 4 g(x) | -4 | 0 | 12

Question 15.

Solution 15.

1. Enter the formula: 2π=1/3 π r^2 h.
2. Solve for h using sliders in Desmos.
3. The height is 6.

Question 16.

Solution 16.

• Graph both equations: 𝑦 = 3 ( 6 𝑥 + 11 ) and 𝑦 = 𝐷 ( 9 𝑥 + 4 ).
• Adjust 𝐷 until the lines are parallel.𝐷 = 2

Question 17.

Solution 17.

• Enter both inequalities.
• Find the overlap region and test points.
• The point that satisfies both is A. (8,4)

Question 18.

Solution 18.

• Enter the list as a = [3, 5, 5, 8, 9, 12, b].
• Add a slider for b.
• Adjust b until mean(a) equals median(a).

Question 19.

Solution 19.

• Enter S=1642⋅3^(nt).
• Set t=0.5 and adjust n until S is three times the initial value. C. 2

Question 20.

Solution 20.

• Enter both equations into Desmos:x+y=80y=2x+8
• Identify the intersection point of the two lines on the graph.
• The y-coordinate of the intersection point is56

Now, how much did you score?

Whether you excelled or struggled, the journey to mastering the SAT is one where targeted support can make all the difference. At Thriving Scholars, our diligent team leverages modern approaches and perfectly curated digital tools that mimic the College Board prep style to ensure your success. From mastering essential Desmos skills like solving equations, finding intercepts, and analyzing inequalities, to tackling challenging SAT-style problems, this blog post has explored the power of Desmos in simplifying even the toughest questions.

With a focus on hands-on practice and real-world problem-solving, these strategies can help you gain confidence and accuracy. Learn more about our Digital SAT Online Tutoring and how we can guide you to assured results by visiting Thriving Scholars. Let us help you maximize your potential and achieve your dream score! 10 Hardest DIGITAL SAT Math Questions

Best Digital SAT Online Classes

Click here to attempt the 10 Hardest Digital SAT Questions of 2025